Allgemeines zur Operationsvorstellung
Kinder mit Schwierigkeiten beim Mathematiklernen haben meist ein einseitig ausgebildetes Operationsverständnis. Für sie ist Mathematik mitunter eine „Welt voller geheimnisvoller Ziffern und Zeichen, die auf noch geheimnisvollere Art und Weise regelhaft miteinander verknüpft werden müssen.“ (Schipper 2005, S. 53) Zu diesen Zeichen zählen neben Zahlen auch die Operationszeichen - plus, minus, mal und geteilt.
Wenn Kinder Rechenverfahren zwar durchführen können, aber Schwierigkeiten mit der Übersetzung einer Rechenaufgabe in Bilder oder Handlungen haben, deutet dies darauf hin, dass sie noch nicht verstanden haben was mit dem Operationszeichen überhaupt gemeint ist. Eine Operation wird von ihnen nicht als Handlung verstanden, sondern das Zeichen als Algorithmus, als bloße Aufforderung zum Rechnen. Für den Aufbau von Grundvorstellungen zählt als „Grundidee […], dass konkrete Handlungen an geeigneten Materialien zu gedanklichen Operationen umgebaut werden.“ (Wartha/ Schulz 2011, S. 11)
Woran erkennt man nicht tragfähige Operationsvorstellungen
Eine mögliche Diagnose für einseitige und nicht tragfähig ausgebaute Operationsvorstellungen sind Aufgaben, bei denen Kinder eine Rechnung erklären sollen, z.B. in Form einer „Indianergeschichte“. Hierbei soll ein Kind einem Indianerkind, das die deutsche Sprache nicht spricht und versteht und weder Zahlen noch Rechenoperationen kennt, erklären was z.B. 2 · 5 ist. Die Darstellungen, die Kinder wählen, sagen viel über ihre Operationsvorstellung aus. (vgl. Schipper 2005, S. 53ff.)
Beispielhaft für einseitige Operationsvorstellungen ist, dass Kinder auf die reine Rechnung zurückgreifen (vgl. Abb. 1). Hier zeichnet ein Kind für die Darstellung sowohl den Multiplikator (2), als auch den Multiplikanden (5) als Menge und verbindet diese als Malaufgabe durch ein Mal-Zeichen. Das Ergebnis ist in dieser Darstellung nicht erkennbar.

Abb. 1: Schülerdarstellung zu der Aufgabe 2 · 5
(In Anlehnung an: Schipper 2005, S. 55)
Flexible und tragfähige Operationsvorstellungen
Wichtig sind tragfähige Operationsvorstellungen, da es beim Rechnen nicht nur um das Einüben nicht-verstandener Rechenregeln geht. Auch diese mechanische Seite des Rechens muss gelernt werden, die Rechenoperationen müssen darüber hinaus aber auch verstanden werden und Vorstellungen dafür entwickelt werden, was sie bedeuten.
Das Üben und schlussendlich Automatisieren von Aufgaben, z.B. des kleinen Einmaleins als auswendiggelernte, abrufbare Aufgaben, findet seine Berechtigung, jedoch muss für ein tiefes mathematisches Verständnis vorab verstanden werden, welche dynamische Handlung bzw. statische Anordnung hinter 3 · 5 steht, bevor die Kinder das Ergebnis 15 nennen, da sie das Ergebnis automatisiert haben. Mit einer Vorstellung von der Bedeutung der Rechenoperationen und dem Verständnis für Zusammenhänge zwischen Aufgaben können Kinder Rechenaufgaben leichter und dauerhaft lernen und sich merken. (vgl. Gaidoschik 2007, S. 69f.)
Die verschiedenen Grundvorstellungen zu den vier Operationen können insgesamt statisch (u.a. Zusammenfassen, Vergleichen) oder dynamisch (u.a. Hinzufügen, Wegnehmen, Ergänzen) sein.
Wenn Kinder die Rolle der Lehrkraft einnehmen sollen, die erklärt was „plus“ bedeutet, kann viel darauf geschlossen werden, wie die Operationsvorstellungen der Kinder ausgebildet sind. Zeigt das Kind seine Finger und zählt entsprechend Finger hinzu oder ab kann von einer dynamischen Vorstellung gesprochen werden. Werden Objekte nebeneinandergelegt und vereinigt, ist die Vorstellung eher statisch. Dagegen kann es auch vorkommen das Kinder die Zahlen in Form der Rechnung nebeneinander mit Gegenständen legen (vgl. Abb. 1). Hier kann von einer nicht hinreichend entwickelten Operationsvorstellung ausgegangen werden.
(vgl. Das Recheninstitut zur Förderung mathematischen Denkens o.J.)
Entwicklung der Operationsvorstellungen
Die Entwicklung der Grundvorstellungen kann anhand von Handlungen am Material, der flexiblen Interpretation von Darstellungen sowie anhand von Sachkontexten gelingen. Durch „Übersetzungen“ von konkreten Handlungen (in Sachkontexten) oder an geeigneten Anschauungsmitteln und Schrift und umgekehrt wird ein Verständnis für Rechenzeichen aufgebaut. Eine Handlung mit Material allein entwickelt jedoch noch keine tragfähige Vorstellung, sondern erst das Nachdenken darüber. Außerdem muss die Handlung mit Material von der Lehrkraft unterstützt werden, da es sonst sein kann, dass Kinder ausschließlich zählend mit den Materialien rechnen und vorhandene Strukturen nicht ausnutzen. Mit verdecktem Material zu arbeiten und dies auch sprachlich zu beschreiben – also mentale Konstruktionen zu verinnerlichten Handlungen zu nutzen – bilden Operationsvorstellungen aus. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 29)
Auch verschiedene Grundvorstellungen zu einer Operation zu entwickeln ist im Unterricht von Bedeutung, damit z.B. nicht nur dynamische, sondern auch statische Situationen durchdrungen werden. Wird beispielsweise die Subtraktion ausschließlich als Wegnehmen verstanden, kann das zum Problem werden, wenn z.B. Sachaufgaben eine andere Grundvorstellung ansprechen. Indem Kinder Sachaufgaben bzw. Rechengeschichten mit vielfältigen Sachkontexten kennenlernen, kann hier entgegengewirkt werden. (vgl. ebd., S. 29)
 Abb. 2: Mehrdeutige Abbildung. Statt 7-3 lässt sich auch 3+4 und 7-4 erkennen.
Abb. 2: Mehrdeutige Abbildung. Statt 7-3 lässt sich auch 3+4 und 7-4 erkennen.(In Anlehnung an: Gaidoschik 2007, S. 79)
Neben Handlungen fördern das Besprechen, Beschreiben und Interpretieren von Darstellungen und Handlungen zu Rechnungen die tragfähigen Operationsvorstellungen (vgl. ebd., S. 30). Z.B. kann die Rechenaufgabe 5 + 4 schrittweise mit den Sätzen „Zuerst habe ich 5 Finger dann gebe ich noch 4 Finger dazu. Insgesamt habe ich dann 9.“ verknüpft werden. Die Verbindung mathematischer Symbole mit realen Situationen vertieft das Verständnis für die Handlung. (vgl. Gaidoschik 2007, S. 74f.)
Des Weiteren eignen sich Abbildungen für den Aufbau von Operationsvorstellungen. Darstellungen können jedoch nicht für sich stehen und sind erst recht nicht eindeutig (vgl. Abb. 2). Zu einer Abbildung finden Kinder verschiedenste Rechnungen, die mit einer entsprechenden Begründung alle ihre Berechtigung haben können.
Deshalb ist es sinnvoll Kinder Abbildungen selbst deuten zu lassen und keinesfalls eine Deutung als „die richtige“ vorzugeben. Auch das eigene Anfertigen von Abbildungen kann für Kinder die Vorstellung einer Operation vertiefen. (vgl. Gaidoschik 2007, S. 79f.)
Gleichungen als Anlass zum Rechnen
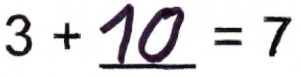 Abb. 3: Typische fehlerhafte Lösung.
Abb. 3: Typische fehlerhafte Lösung.(In Anlehnung an: Gaidoschik 2007, S. 155)
Im Zusammenhang mit Operationsvorstellungen hat das Gleichzeichen eine besondere Bedeutung. Während das Zeichen oft in erster Linie als Aufforderung zum Rechnen interpretiert wird, ist es für Kinder bereits in der Grundschule wichtig die Bedeutung des Gleichzeichens zu verstehen. Die Gleichwertigkeit beider Seiten der Gleichung kann z.B. als Waage veranschaulicht werden. Dass nicht bei jedem Gleichzeichen sofort eine Rechnung abgerufen wird, ist für eine tragfähige Operationsvorstellung von Nöten. (vgl. ebd., S. 154ff.)
Austausch mit anderen Kindern
Wichtig für die Entwicklung von Vorstellungen zu allen Operationen ist, dass Kinder mit und ohne Schwierigkeiten beim Mathematiklernen für sich Vorstellungen zu den Operationen und den damit verbundenen Handlungen aufbauen. Anschließend müssen ihnen weitere Vorstellungen aufgezeigt werden, die zu den Operationen ebenfalls existieren. Dies kann über den Austausch mit anderen Kindern geschehen, die eine alternative Vorstellung haben. Damit erweitern sie ihr eigenes Wissen und verbalisieren außerdem ihre eigenen Denkweisen. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 37)
Andernfalls kann es sein, dass Kinder eine Operation als Algorithmus lernen ohne die Operation zu verstehen. Das Ziel des Mathematikunterrichts ist die flexible Darstellung und Vorstellung der Operationen. (vgl. ebd., S. 29f.)
Literatur:
Das Recheninstitut zur Förderung mathematischen Denkens (Hrsg.) (o.J.): Typische Schwierigkeiten im 2.Schuljahr.
http://www.recheninstitut.at/mathematische-lernschwierigkeiten/merkmale/typische-schwierigkeiten-im-2-schuljahr/ [07.05.2017]
Gaidoschik, Michael (2007): Rechenschwäche vorbeugen - Erstes Schuljahr: Vom Zählen zum Rechnen. Wien: ÖBV HPT.
Häsel-Weide, Uta/ Nührenbörger, Marcus (2012): Fördern im Mathematikunterricht. In: Bartnitzky, Horst/ Hecker, Ulrich/ Lassek, Maresi (Hrsg.): Individuell fördern – Kompetenzen stärken – in der Eingangsstufe (Kl. 1 und 2) (Vol. 134, Heft 4). Frankfurt am Main: Grundschulverband.
Schipper, Wilhelm (2005): Modul G4: Lernschwierigkeiten erkennen - verständnisvolles Lernen fördern. Kiel.
Wartha, Sebastian/ Schulz, Axel (2013): Rechenproblemen vorbeugen. 2. Auflage, Berlin: Cornelsen.
Weiterführende Literatur und Linktipps:
Zur Vorgehensweise und Strategien bei Additions- und Subtraktionsaufgaben von Erstklässlern
Dieses Fördermaterial setzt den Fokus auf den Wechsel zwischen den verschiedenen Darstellungsformen (Aufgabe – mathematische Handlung am Material – Bild – Rechengeschichte).
Vorstellungen zur Addition & Subtraktion
Im Anfangsunterricht sind Addition und Subtraktion die zentralen Operationen, zu denen Kinder Vorstellungen entwickeln müssen. Schon vor ihrem Schuleintritt können viele Kinder addieren und subtrahieren und dabei mit Materialien oder unter Zuhilfenahme ihrer Finger dynamische Sachprobleme lösen. Neben dynamischen werden jedoch auch statische Vorstellungen zur Addition und Subtraktion für die Entwicklung eines tiefen mathematischen Verständnisses benötigt. In der Schule wird das Vorwissen weiterentwickelt und die Rechnung mit Materialien durch die abstrakten Zahlen und mathematischen Symbole für plus und minus ergänzt, um mit ihnen die selben Sachsituationen zu lösen. (vgl. Gaidoschik 2007, S. 70f.)
Problematisch ist es, wenn Addition und Subtraktion ausschließlich als Vor- bzw. Rückwärtszählen verstanden wird, denn ein umfassendes, vielfältiges Verständnis für die Operationen lässt sich dabei nur schwer entwickeln. Dies wird auch bei Sachsituationen deutlich, in denen Rechenoperationen nicht nur einseitig aktiviert werden sollen, sondern flexibel eingesetzt werden müssen. (vgl. Wartha/ Schulz 2013, S. 48)
Grundvorstellungen der Addition
Die Addition besitzt verschiedene Grundvorstellungen. Zum einen kann dynamisch eine Menge „hinzugefügt“ oder statisch Mengen „zusammengefasst“ werden (vgl. Abb. 4).
Die Ausbildung der Operationsvorstellung kann durch Übersetzungen von Rechenaufgaben in Handlungen, Darstellungen und Versprachlichungen und umgekehrt geschehen. Für jede Rechenaufgabe gibt es eine Vielzahl von möglichen Darstellungen und Handlungen. Die „eine“ Abbildung einer Additionsaufgabe gibt es dagegen nicht. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 29f.)
Für die Anregung der Operationsvorstellungen zur Addition sind zunächst die „einfachen“ Additionsaufgaben eine Stütze, die Kinder nutzen können. Dazu gehören Aufgaben, die sie beherrschen, wie Verdopplungsaufgaben, die Addition zu 10 oder die Addition eines glatten Zehners. Da diese Aufgaben oft gedächtnismäßig im Anfangsunterricht beherrscht werden, kann daran angeknüpft werden. Wird auf diese Aufgaben zurückgegriffen, können mit „1 weg“ oder „1 dazu“ weitere Aufgaben erschlossen werden. Dadurch, dass die Handlungen mental vorgestellt werden, werden die Operationsvorstellungen der Kinder weiter ausgebildet. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 30f.)
|
Darstellung 1 |
Grundvorstellung |
Darstellung 2 |
|---|---|---|
|
Andrea hat 5 Plättchen. Sie bekommt 3 dazu. Wie viele Plättchen hat sie jetzt? |
+ als Hinzufügen |
5 + 3 |
|
Sonja hat 5 Plättchen. Pascal hat 3. Wie viele Plättchen haben sie zusammen? |
+ als Zusammenfassen |
5 + 3 |
|
Michael bekommt 5 Plättchen von Axel und 3 von Claus. Wie viele hat er insgesamt bekommen? |
+ als Zusammenfassung zweier Änderungen |
5 + 3 |
|
|
- als Wegnehmen |
11 - 4 |
|
Alex hat 11 Plättchen. Tom hat 9.Wie viele Plättchen muss Tom noch bekommen, damit er genauso viele Plättchen hat wie Alex. |
- als Ergänzen |
11 - 9 |
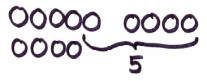 |
- als Vergleichen |
9 - 4 |
|
Zusammen haben Helena und Melanie 11 Plättchen. Melanie hat 6. Wie viele hat Helena? |
- als Umkehrung von + |
11 - 4 |
Abb. 4: Grundvorstellungen zu Operationen Addition und Subtraktion.
(In Anlehnung an: Wartha/ Schulz 2013, S. 31)
Grundvorstellungen der Subtraktion
Die Subtraktion bietet drei verschiedene Operationsvorstellungen. Beim „Wegnehmen“ wird dynamisch der Subtrahend vom Minuenden abgezogen, während beim „Vergleichen“ statisch die Differenz zwischen Minuend und Subtrahend betrachtet wird (vgl. Abb. 4). „Ergänzen“ greift eine additive Vorstellung auf. Obwohl diese Grundvorstellung weniger häufig genutzt wird, ist sie bei einigen Aufgaben geschickt. So kann bei 65 - 63 über eine Ergänzung das Ergebnis berechnet werden, auf das man durch Wegnehmen wesentlich aufwändiger käme. Zur Veranschaulichung des Ergänzens kann z.B. der Rechenstrich genutzt werden, der den Schritt von Minuend und Subtrahend veranschaulicht. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 35f.)
Subtraktion veranschaulichen
Bei Darstellungen der Grundvorstellung „Wegnehmen“ besteht die Schwierigkeit darin, alle drei Teilmengen so darzustellen, dass sie sichtbar bleiben. Wird jedoch von der Ausgangsmenge etwas weggenommen, bspw. Wendeplättchen, so lässt sich die Ausgangsmenge nicht mehr erkennen, wenn die Operation durchgeführt wurde. Während bei der Addition (z.B. 4 + 3) beide Mengen nebeneinander gelegt werden können, sind bei 4 - 3 letztere 3 nicht mehr da. Die Abbildung ist wesentlich schwieriger mit der Aufgabe in Verbindung zu bringen. In Darstellungen wird oft auf ein angedeutetes Wegnehmen, durchgestrichene Plättchen oder leicht durchsichtige Folien über Plättchen (vgl. Abb. 5) zurückgegriffen. Hierdurch wird der Subtrahend abgedeckt ohne den Minuenden aufzulösen. Auch bei diesen Darstellungen, die für ein geschultes Auge eindeutig als Subtraktion zu erkennen sind, müssen Kinder das „Lesen“ der Darstellung erst erlernen. Mit Handlungen und Sprechen kann dies gelingen. (vgl. Häsel-Weide/ Nührenbörger 2012. In: Bartnitzky/ Hecker/ Lassek, S. 32f.)
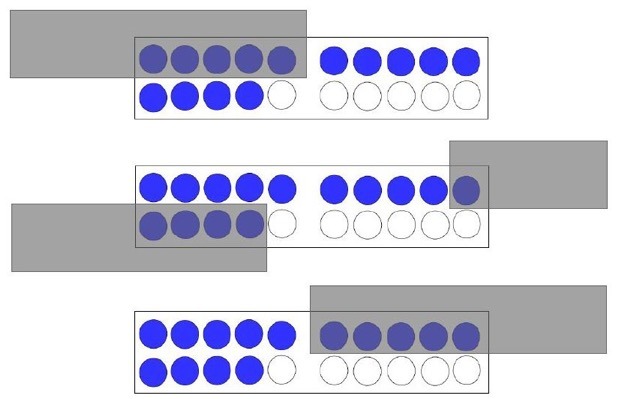
Abb. 5: Verschiedene Darstellung der Subtraktionsaufgabe 14 – 5 = 9 durch transparente Folien über Plättchen.
(In Anlehnung an: Häsel-Weide /Nührenbörger 2012 In: Bartnitzky/ Hecker/ Lassek, S. 33)
Nachdem Grundvorstellungen der Addition und Subtraktion ausgebildet wurden, sind Verdoppeln und Halbieren als Vorreiter von Multiplikation und Division für ein tiefes mathematisches Verständnis notwendig. (vgl. ebd., S. 29)
Literatur:
Häsel-Weide, Uta/ Nührenbörger, Marcus (2012): Fördern im Mathematikunterricht. In: Bartnitzky, Horst/ Hecker, Ulrich/ Lassek, Maresi (Hrsg.): Individuell fördern – Kompetenzen stärken – in der Eingangsstufe (Kl. 1 und 2) (Vol. 134, Heft 4). Frankfurt am Main: Grundschulverband.
Wartha, Sebastian/ Schulz, Axel (2013): Rechenproblemen vorbeugen, 2. Auflage, Berlin: Cornelsen.
Weiterführende Literatur und Linktipps:
Zur Diagnose und Förderung bietet das Material „Mathe sicher können. Handreichung für ein Diagnose- und Förderkonzept zur Sicherung mathematischer Basiskompetenzen“ mögliche Aufgaben um Operationsvorstellungen zu diagnostizieren und zu fördern.
Vorstellungen zur Multiplikation & Division
Schon bevor mit Kindern Multiplikation und Division im Unterricht thematisiert wurde, können sie durch ihr Vorwissen bereits Sachaufgaben dazu lösen. Noch ohne tragfähige Operationsvorstellungen kommen sie oft zu Lösungen, indem sie direkt mit Materialien modellieren und anschließend auszählen. Mit anderen Strategien – z.B. rhythmischem Zählen, gelernten Zahlenfolgen sowie Verknüpfungen zur Addition bei Multiplikationsaufgaben bzw. wiederholten Subtraktionen und Verknüpfungen zur Multiplikation bei Divisionsaufgaben – lösen dagegen einige Kinder die Aufgaben mit Vorkenntnissen, die auf ein Operationsverständnis hindeuten. (vgl. Padberg 2009, S. 114ff.; ebd., S. 138ff.)
Tragfähige und vielfältige Vorstellungen zur Multiplikation und Division müssen im Unterricht ausgebildet werden und stellen für Kinder auch am Ende der Grundschulzeit oft noch eine Herausforderung dar. Alle Kinder, ob mit oder ohne Schwierigkeiten beim Mathematiklernen, benötigen zur Entwicklung tragfähiger Operationsvorstellungen Handlungserfahrungen sowie Möglichkeiten diese zu versprachlichen und zu verinnerlichen. (vgl. Gaidoschik 2009, S. 50)
Zur Diagnose der Kenntnisstände der Kinder eignen sich Aufgaben mit Kontexten der Lebenswirklichkeit der Kinder und offene Aufgaben, die verschiedene Bearbeitungswege und Ergebnisse zulassen und damit vielfältig gelöst werden können. An die genutzten Lösungsstrategien der Kinder kann der Aufbau bzw. die Weiterentwicklung der Grundvorstellungen ansetzten.
Operationsvorstellung zur Multiplikation
In Schulbüchern werden Multiplikationsaufgaben oft sowohl als „zeitlich-sukzessive Handlung“ (vgl. Abb. 6), als auch als „räumlich-simultane Anordnung“ (vgl. Abb. 7) abgebildet.

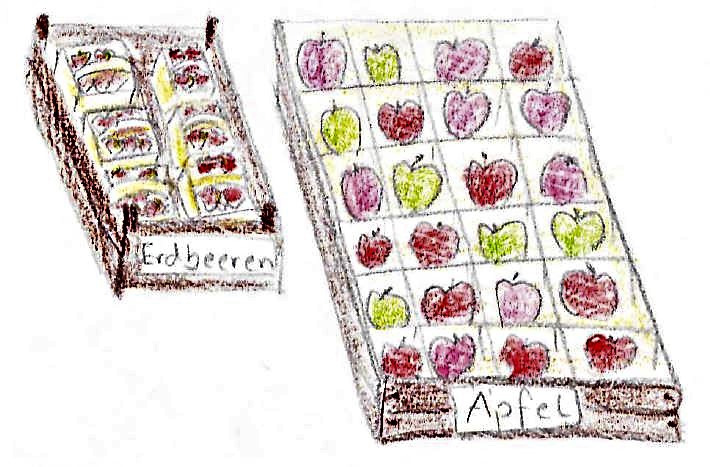 Abb. 6: Beispiel der Multiplikation als "zeitlich-sukzessive Handlung" Abb. 7: Beispiel der Multiplikation als "räumlich-simultane Anordnung"
Abb. 6: Beispiel der Multiplikation als "zeitlich-sukzessive Handlung" Abb. 7: Beispiel der Multiplikation als "räumlich-simultane Anordnung"
Darüber hinaus ist auch eine Vorstellung der Multiplikation im kombinatorischen Kontext möglich.
Bei der dynamischen Vorstellung einer zeitlich-sukzessiven Handlung zur Multiplikation entsteht die Gesamtmenge bzw. das Produkt durch mehrmalige Wiederholungen derselben Handlung, bei der eine gleichmächtige Menge hinzugefügt wird, z.B. indem dreimal 5 Äpfel geholt werden. Hier wird der Zusammenhang zwischen der vielfachen Addition und der Multiplikation besonders deutlich. Durch den alltäglichen Gebrauch von z.B. „dreimal“ ist für Kinder diese Vorstellung oft sehr alltagsnah. (vgl. Padberg 2009, S. 117f.)
Räumlich-simultane Anordnungen dagegen bilden statisch eine Gesamtmenge als mehrere gleichmächtige Mengen ab. Hierbei werden die Mengen statisch zusammengefügt, was ebenfalls mit der statischen Grundvorstellung der Addition („Zusammenfügen“) in Verbindung gebracht werden kann. Die räumlich-simultane Anordnung kann auch als Ergebnis der zeitlich-sukzessiven Handlung gesehen werden und begründet den engen Zusammenhang beider Vorstellungen. Wichtig ist, dass Kinder bei beiden Situationen Multiplikationsaufgaben erkennen können. (vgl. ebd., S. 118f.)
Eine andere Vorstellung der Multiplikation spricht die Kombinatorik an. Werden z.B. alle Möglichkeiten für zweigängige Menüs gesucht, bei den aus 3 Vorspeisen und 5 Hauptgerichten gewählt wird, kann mit 3 · 5 die Kombinationsanzahl bestimmt werden. Hier sind für die zwei Vorspeisen jeweils 5 Hauptgerichte möglich. Diese Vorstellung ist für die Einführung der Multiplikation nicht sinnvoll, da die Arbeit mit Materialien und Darstellungen schwieriger ist. Für Sachprobleme ist der kombinatorische Aspekt der Multiplikation jedoch unabdingbar. (vgl. ebd., S. 120f.)
Operationsvorstellung zur Division
Nachdem die Multiplikation thematisiert wurde, sollte davon getrennt die Division im Unterricht eingeführt werden. Sie kann als Aufteil- oder Verteil-Situation gedeutet werden.
Beim Aufteilen wird die Gesamtmenge in Teilmengen aufgeteilt, die eine bekannte gleichmächtige Anzahl haben. Beispiel hierfür kann eine Kindergruppe sein mit insgesamt 6 Kindern, die in Dreiergruppen aufgeteilt wird. Die Anzahl der Kleingruppen (2) entspricht dem Ergebnis. Gesucht ist beim Aufteilen die Anzahl der Teilmengen, während die Gesamtmenge (6) und die Gruppengröße (3) gegeben ist (vgl. Abb. 8).
Abb. 8: Beispiel der Division als "Aufteilen"
Diese Art der Vorstellung ist alltagsnah und anschaulich und zeigt gleichzeitig einen Zusammenhang zur Multiplikation, wenn die Gruppen räumlich-simultan angeordnet wurden. (vgl. ebd., S. 141f.)
Beim Verteilen ist im Gegensatz dazu die Anzahl der Teilgruppen bekannt und die Elementzahl der Teilmengen wird gesucht. Beispiel dafür kann das Verteilen von 16 Murmeln an 4 Kinder sein. Aufgaben, die diese Vorstellung ansprechen, bieten Handlungen mit Materialien an, bei denen z.B. Murmeln einzeln oder in Schritten verteilt werden (vgl. Abb. 9).

Abb. 9: Beispiel der Division als "Verteilen"
Wichtig ist, dass bei Sachkontexten eine gerechte Teilung gefragt ist, die sich allein auf die Anzahl bezieht und nicht z.B. zwei kleine Murmeln mit einer großen gleichsetzt.
Das Verteilen eignet sich auch, um die Division mit Rest zu verdeutlichen. Werden beispielsweise 22 Murmeln an 5 Kinder verteilt, wird durch die Handlung ersichtlich, dass dies nicht restlos geschehen kann. (vgl. ebd., S. 143f.)
Entwicklung von Grundvorstellungen
„Das kleine Einmaleins muss man sich doch einfach merken“ (Gaidoschik 2009, S. 52) heißt es immer wieder und ein Ziel des Unterrichts ist natürlich auch, dass Kinder die Aufgaben des kleinen Einmaleins automatisiert abrufen können. Jedoch sollte dies nicht dadurch geschehen, dass die einzelnen Reihen in Art eines Gedichts auswendig gelernt werden. Stattdessen soll das Abrufen am Ende eines verständnisaufbauenden Unterrichts stehen. Sonst werden die einzelnen Aufgaben nur solange beherrscht, wie die Reihen auswendig gelernt werden und geraten nach einiger Zeit in Vergessenheit. (vgl. ebd., S. 52)
Gerade das Auswendiglernen führt oft dazu, dass Kinder mit Schwierigkeiten beim Mathematiklernen bei der Einführung der Multiplikation gute Leistungen zeigen. Das Abrufen der Aufgaben bzw. das Hochzählen der Reihen beherrschen sie, jedoch ist nur eine tragfähige Operationsvorstellung nachhaltig für mathematisches Verständnis. (vgl. Häsel-Weide/ Nührenbörger 2013 In: Bartnitzky/ Hecker/ Lassek, S. 35)
Um die verschiedenen Grundvorstellungen zu Multiplikation und Division zu erlernen, ist für alle Kinder das Handeln mit Materialien unverzichtbar. Die konkreten Vervielfachungen einer Handlung z.B. wenn vier mal 5 Murmeln geholt werden, lassen Kinder die Vorstellung einer zeitlich-sukzessiven Multiplikation erfahren. Die Übersetzung der Handlung in eine sprachliche Form („vier mal fünf Murmeln“) und zuletzt in einen Rechenterm (4 · 5) und die Rück-Übersetzungen, fördern das Verständnis der Multiplikation. (vgl. Gaidoschik 2009, S. 53)
Das genutzte Material muss in Hinblick auf den höheren Zahlenraum und auf eine Struktur hin ausgewählt werden. Damit nicht wiederholt abgezählt werden muss, aber trotzdem mehrdeutige und flexible Darstellungen gefunden werden können, eignen sich z.B. besondere Punktestreifen um eine Multiplikation darzustellen (vgl. Abb. 10). Hierbei wird mit gleichmächtigen Mengen (Punktestreifen mit jeweils gleich vielen Punkten) umgegangen, diese genutzt, um Handlungen durchzuführen (mehrere Punktestreifen hinzufügen und abziehen) und sich zunehmend von den Handlungen gelöst und sie stattdessen verdeckt oder mental durchgeführt. Die Punktestreifen können als Darstellung einer Multiplikation als Punktereihen oder als Punktefelder angeordnet und gedeutet werden. Mit flächigen Punktefeldern wird z.B. die spätere geometrische Flächenberechnung vorbereitet. (vgl. Häsel-Weide/ Nührenbörger 2013 In: Bartnitzky/ Hecker/ Lassek, S. 36)
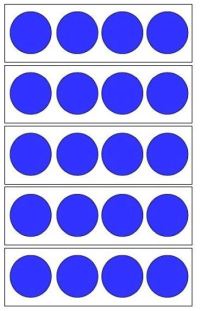
Abb. 10: Punktestreifen mit jeweils 4 Punkten können eingesetzt werden, um Multiplikationen darzustellen, wie hier 5 · 4.
Literatur:
Häsel-Weide, Uta/ Nührenbörger, Marcus (2013): Fördern im Mathematikunterricht. In: Bartnitzky, Horst/ Hecker, Ulrich/ Lassek, Maresi (Hrsg.): Individuell fördern - Kompetenzen stärken ab Klasse 3 (Vol. 135, Heft 2). Frankfurt am Main: Grundschulverband.
Gaidoschik, Michael (2009): „Das muss man sich einfach merken“??? - Schwierigkeiten mit dem Einmaleins: Einige Anregungen für Vorbeugung und Abhilfe. Wien. http://www.recheninstitut.at/mathematische-lernschwierigkeiten/fordertips/einmaleins/ [05.07.2015]
Padberg, Friedhelm (2009). Didaktik der Arithmetik. Für Lehrerausbildung und Lehrerfortbildung (3. erweiterte, völlig überarbeitete Auflage). Heidelberg: Spektrum Akademischer Verlag.


